O Modelo Black & Scholes
O modelo de Black & Scholes é de longe o mais utilizado no mercado, principalmente pela simplicidade e facilidade com que pode ser implementado, até mesmo em uma calculadora HP.
Uma forma intuitiva de se compreender o funcionamento do modelo de Black & Scholes pode ser o preço de uma opção de compra (call), por exemplo, pode ser visto como uma esperança matemática, onde N(d1) é a probabilidade do preço do ativo chegar ao vencimento acima do preço de exercício ( X), e N(d2) é a probabilidade do preço do ativo cair abaixo do atual preço de mercado ( S). N(d1) é a probabilidade de um ganho ilimitado, caso o preço do ativo suba, e N(d2), de uma perda limitada, caso caia. A soma dessas duas probabilidades é que dará o valor no tempo da opção.
No momento do vencimento, N(d1) e N(d2) serão ambas iguais a 1, caso a opção termine em exercício, ou iguais a zero, caso “vire pó”. Nesse caso o preço da opção de compra será inteiramente o do valor intrínseco ( max [ S- X,0 ]), e o valor no tempo terá sido totalmente corroído.
A formula de Black & Scholes para o preço de uma call é a seguinte:
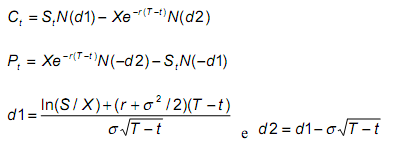


Destacamos que de todos os parâmetros que determinam o preço de uma opção, a volatilidade é o que representa maiores problemas. Todas as outras variáveis são dadas (preço de exercício, preço a vista, tempo até o vencimento), ou podem facilmente ser estimadas (dividendos esperados, taxa de juros sem risco) a partir de algumas observações. Já a volatilidade, representa maiores problemas, pois não é uma variável diretamente observável. Isso implica que se todos os outros parâmetros forem vistos da mesma maneira pelos diversos agentes do mercado, o que os fará ter diferentes expectativas de preço para a opção serão as diferentes formas de enxergarem esse parâmetro de volatilidade. Várias abordagens podem ser utilizadas na sua estimação. Por ora, basta ficar a noção de que este é o parâmetro mais crítico na etapa de precificação, e que a melhor estimativa da “verdadeira” volatilidade, dará a melhor estimativa de preço para a opção, permitindo maior aproximação do preço ajustado, e portanto, melhores possibilidades na identificação das oportunidades de lucro no mercado.
Neste tópico serão tratados os instrumentais teóricos utilizados para avaliar a sensibilidade dos preços dos contratos de opções as diversas variáveis que influenciam seus prêmios. São as sensibilidades dos preços das opções, ou os chamados “gregas“.
Trata-se exclusivamente de medidas de curto prazo que podem ser utilizadas para controlar a exposição das posições financeiras a vários tipos de risco*, ou de instrumentos semelhantes ao painel de controle de uma aeronave, que dariam ao piloto condições de conduzir o avião em situações meteorológicas adversas, quando o contato visual não é possível. Nessa linha nenhum piloto que se preze, mesmo com tempo bom, deixaria de olhar pela janela ao pilotar, até mesmo porque alguns instrumentos podem falhar. Não é demais lembrar que em aviação, o real vôo cego, é aquele onde os instrumentos da cabine deixam de funcionar, e não é aquele em que se tem que aproximar da pista de pouso sem contato visual.
* Risco de mudança na taxa de juro, na volatilidade do ativo, ou de alta ou de baixa no preço do ativo, entre outros.
Mercado de Opções, leia mais
- Estratégia de opções: Borboleta Assimétrica
- Estratégia de opções: Mesa (condor)
- Estratégia de opções: Borboleta
- Estratégia de opções: Trava de Baixa (Reversão)
- Estratégia de opções: Trava de Alta
- Estratégia lançamento (venda) coberto de opções
- Estimativas e Simulações no mercado de opções
- Fatores que afetam o preço de uma opção
- Porque investir no Mercado de Opções
- Mercado de Opções
- Venda Coberta: Como definir a melhor taxa
- Ajustes de operações com opções
- Hedge com Opções
- Operando Opções com posições neutras
- Volatilidade Implícita das opções
- As Gregas do Modelo Black & Scholes
- Black & Scholes
- O cálculo do preço das opções
- Valor Intrínseco e Expectativas Futuras nas opções
- Opções Dentro, Fora e No Dinheiro (ITM, OTM e ATM)
- Garantias do Mercado de Opções
- Exemplo de Hedge com opção de venda
- Exemplo de Hedge com opção de compra
- Aplicações do Mercado de Opções
- Definições e termos do mercado de opções
- Classificação e Tipos de Opções
- FIIs de tijolos ou papeis, quais as diferenças? - 11/01/2023
- O que são Fundos Imobiliários - 10/01/2023
- Os Padrões Gráficos da Análise Técnica - 20/06/2020

Muito bom esse conteúdo sobre opções